Angle
subs. masc.
 Espace indéfini compris entre deux plans ou surfaces qui se rencontrent.
Espace indéfini compris entre deux plans ou surfaces qui se rencontrent.
Ces derniers prennent le nom d'angles dièdses.
Le point de rencontre des deux lignes ou des deux plans est le sommet de l'angle.
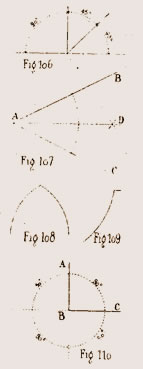
La mesure des angles se compte en degrés à l'aide du rapporteur. (Vov. ce mot). Fig. 106.
On désigne un angle par la lettre du sommet ou par les trois lettres des côtés en plaçant celle du sommet au milieu.
La ligne A D (fig. 107) qui divise un angle C A B en deux parties égales se nomme bissectrice.
Un angle formé de lignes droites C A B (fig. 107) est un angle rectiligne ; celui qui est formé de lignes courbes est un angle curviligne (fig. 108). Enfin l'angle est mixtiligne quand il a pour côtés une ligne droite et une ligne courbe (Fig. 109).
Quand une droite est perpendiculaire à une autre, ces deux droites forment un angle droit, A B C ; il est égal à 90 degrés ou quart de la circonférence (fig. 109).
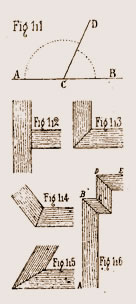 Si les côtés forment un angle D C B de moins de 90 degrés (fig. 111), il prend le nom d'angle aigu ; enfin il est obtus si les côtés forment un angle A C D de plus de 90 degrés (fig. 111).
Si les côtés forment un angle D C B de moins de 90 degrés (fig. 111), il prend le nom d'angle aigu ; enfin il est obtus si les côtés forment un angle A C D de plus de 90 degrés (fig. 111).
L'angle droit prend aussi le nom d'angle d'équerre ou à coupe carrée (fig. 112).
L'angle de 45 degrés ou la moitié de l'angle droit donne la coupe d'onglet (fig. 113).
L'angle aigu prend le nom d'angle maigre, et l'angle obtus, celui de gras. Ces deux derniers angles donnent des angles à fausses coupes (fig. 114 et 115).
Un angle est rentrant quand on considère l'espace compris entre ses côtés ; il est saillant si on considère l'espace qui se trouve en dehors (fig. 116). L'angle B C D est saillant et les deux angles A B C et E D C sont des angles rentrants.
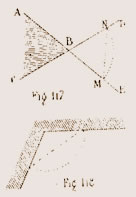 Si l'on prolonge les deux côtés d'un angle, on obtient deux angles qui sont opposés au sommet ; ces deux angles sont égaux ; ainsi, dans la figure 117 l'angle A B C est égal à son prolongement D B E.
Si l'on prolonge les deux côtés d'un angle, on obtient deux angles qui sont opposés au sommet ; ces deux angles sont égaux ; ainsi, dans la figure 117 l'angle A B C est égal à son prolongement D B E.
Le menuisier en prenant des mesures a souvent besoin de relever les angles d'une pièce.
Cette démonstration trouve son application dans le cas d'un angle saillant dont on veut obtenir la mesure pour le reproduire à l'atelier ; soit l'angle saillant A B C formé par un mur : on prolonge le côté A B jusqu'en E et le côté C B jusqu'en D, puis on porte une mesure quelconque lm00 par exemple sur les côtés B D et D E pour fixer les points M N que l'on joint par une ligne droite dont on prend la mesure.
(Les mesures portées sur les côtés prolongés peuvent être différentes). On a ainsi obtenu les données nécessaires à la reproduction de l'angle A B C. L'ouvrier qui est sur le chantier se sert de la fausse équerre ou fait un calibre. (Voy. ces mots)
Pour les angles rentrants, on opère de même quand ils ne sont pas a angle droit ; mais dans ce cas on a la facilité de porter directement les mesures sur les côtés de l'angle formé par le mur (fig. 118).
Nous donnons ci dessous les noms de différents angles dont on trouvera les définitions et les applications à leur ordre alphabétique :
Angle complémentaire.
Angle supplémentaire.
Angles correspondants.
Angle interne.
Angle externe.
Angle alterne interne.
Angle alterne externe. (Voy. ces mots).
L'usage des angles est infini en menuiserie, et on pourrait dire qu'elle ne se compose que d'angles de toutes les formes : Angles des portes, des croisées, des corniches, etc. (Voy. le mot Cadre).
Prix (Voir Bandeau, Arrondissement, Croisée).
Mise à jour 2019-01-04
Lettres
Ce dictionnaire en version papier

